归并排序(含链表)
Posted: 10.21.2019
介绍
较为复杂的排序方法,时间复杂度为 O(nlogn)
时间复杂度很好理解,和快排一样,一共 logn 层,每层比较 O(n) 次
空间复杂度为 O(n) (至于为什么是这样的,后面再解释)
稳定性:稳定
代码实现
核心思想:分治法(Divide and Conquer)
function mergesort(arr) {
mergesortHelper(arr, 0, arr.length - 1);
return arr;
}
// a 和 b 分别指的是两个子数组的起始 index
function mergesortHelper(arr, l, r) {
if (l < r) {
const m = Math.floor((l + r) / 2);
// 对于两个子数组,分别排序
mergesortHelper(arr, l, m);
mergesortHelper(arr, m + 1, r);
// 合并两个子数组
merge(arr, l, m, r);
}
}
function merge(arr, l, m, r) {
// 记录下待会儿要开始复制的位置
const start = l;
// 创建一个暂时的数组,来存储 merge 后的数据
const temp = new Array(r - l + 1);
let index = 0;
let mid = m + 1;
/**
* 在这里,先把 l 和 m 中,某个子数组给全搞到 temp 里
* 结束后,可能会剩下一个子数组还有元素没有复制到 temp 里
*/
while (l < m + 1 && mid <= r) {
if (arr[l] < arr[mid]) {
temp[index] = arr[l];
l++;
} else {
temp[index] = arr[mid];
mid++;
}
index++;
}
// 如果 a 数组还有元素,就复制到 temp 里
while (l < m + 1) {
temp[index] = arr[l];
l++;
index++;
}
// 如果 b 数组还有元素,就复制到 temp 里
while (mid <= r) {
temp[index] = arr[mid];
mid++;
index++;
}
// 把 temp 数组里的数据,复制到原数组里
for (let i = 0; i < temp.length; ++i) {
arr[start + i] = temp[i];
}
}
空间复杂度
大家可以看见,我上面没用 slice,但是有的代码会用到 slice。
slice 和 concat 非常消耗时间与空间,所以我们这里就不看了。
就从上面的方法来看,其总的空间复杂度为 O(n)...
等等,是不是不大对?好像每层都花了 O(n) 的空间啊?
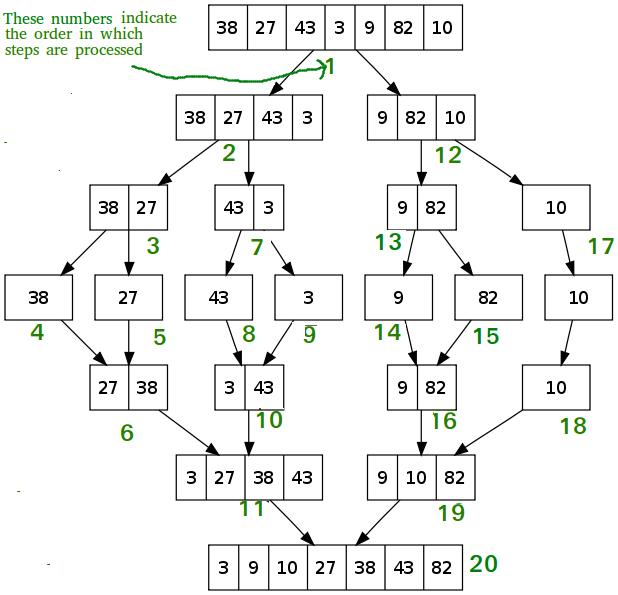
这张图比较直观哈。
结合我们的算法,我们可以发现,在每一层进行合并的时候,我们都创建了一个 temp 的数组。
在每一层,所有 temp 数组加起来,所占据的空间为 O(n),因为我们每一层都合并了 O(n) 个元素(整体来看)。
那么,空间复杂度不应该是 O(nlogn) 吗?为什么是 O(n)?
道理很简单,因为我们每一层,每一层 merge 所需要的空间,并不是平行的,所以不能加起来。
我们就拿这一层为例:
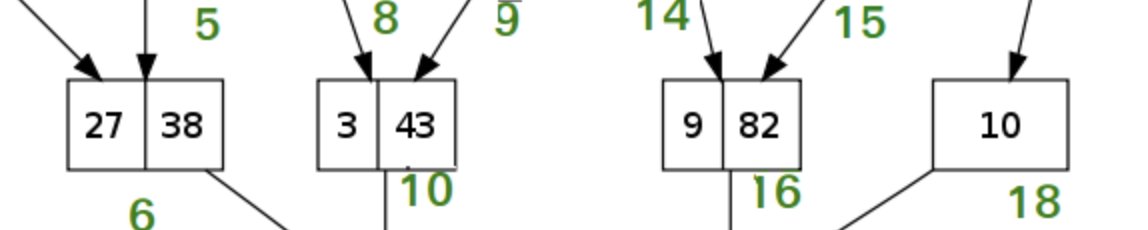
在递归的过程中,这一层实现的顺序是从左往右的。
也就是说,[27, 38] 和 [3, 43] 会首先被合并。
然后 [9, 82] 和 [10] 才会被合并。
这两次操作并不是平行的。
这意味着什么?
意味着,在第一次操作结束后,分配给 temp 的空间会被回收,然后再分配给第二次操作。
在每一层都是这样的。因为操作不是平行的,因此每次操作结束后,空间都会被回收。
等第二次操作需要的时候,空间才会被重新分配。
因此,在每一层,我们所花的空间,就是这一层,每个单独操作所需要的空间。
因此,最终的空间复杂度不是 O(n) + O(n) + ... + O(n) 一直加 logn 个 O(n)。
而是 O(n) + O(n / 2) + O(n / 4) + ... + O(1)。
众所周知,1 + 1/2 + 1/4 + ... + 1/2^logn = 2(别纠结这个式子是不是严谨了,意思大家都懂)。
因此,最后的空间复杂度为 O(n)。
归并排序链表
归并排序链表的思想,其实和数组是一样的。
但我们需要做一些的工作,尤其是 partition 的部分。
function sortList(head) {
// base case
if (!head || !head.next) return head;
// partition
const [left, right] = partition(head);
// 对于两个子链表分别排序
const node1 = sortList(left);
const node2 = sortList(right);
// 合并两个子链表
return merge(node1, node2);
};
function partition(head) {
/**
* partition 的核心思想是快慢指针
* 当快指针抵达链表末尾的时候
* 慢指针抵达了链表的中间(指向第二条链表的开头)
*/
let slow = fast = head,
prev = null;
while (fast) {
prev = slow; // 记录下 slow 前的那个节点
if (slow) slow = slow.next;
if (fast) fast = fast.next;
if (fast) fast = fast.next;
}
/**
* 需要把 slow 前的那个节点的 next 设置成 null
* 这样,我们在排序子链表的时候,才知道在哪里停止
*/
prev.next = null;
return [head, slow];
}
function merge(left, right) {
// edge case
if (!left) return right;
if (!right) return left;
// 通过递归来合并
if (left.val < right.val) {
left.next = merge(left.next, right);
return left;
} else {
right.next = merge(left, right.next);
return right;
}
}
