Lynch

寻找两个有序数组的中位数

Posted: 09.20.2019

#LeetCode #Top 100 Liked #分治法 #面试问题 - 算法

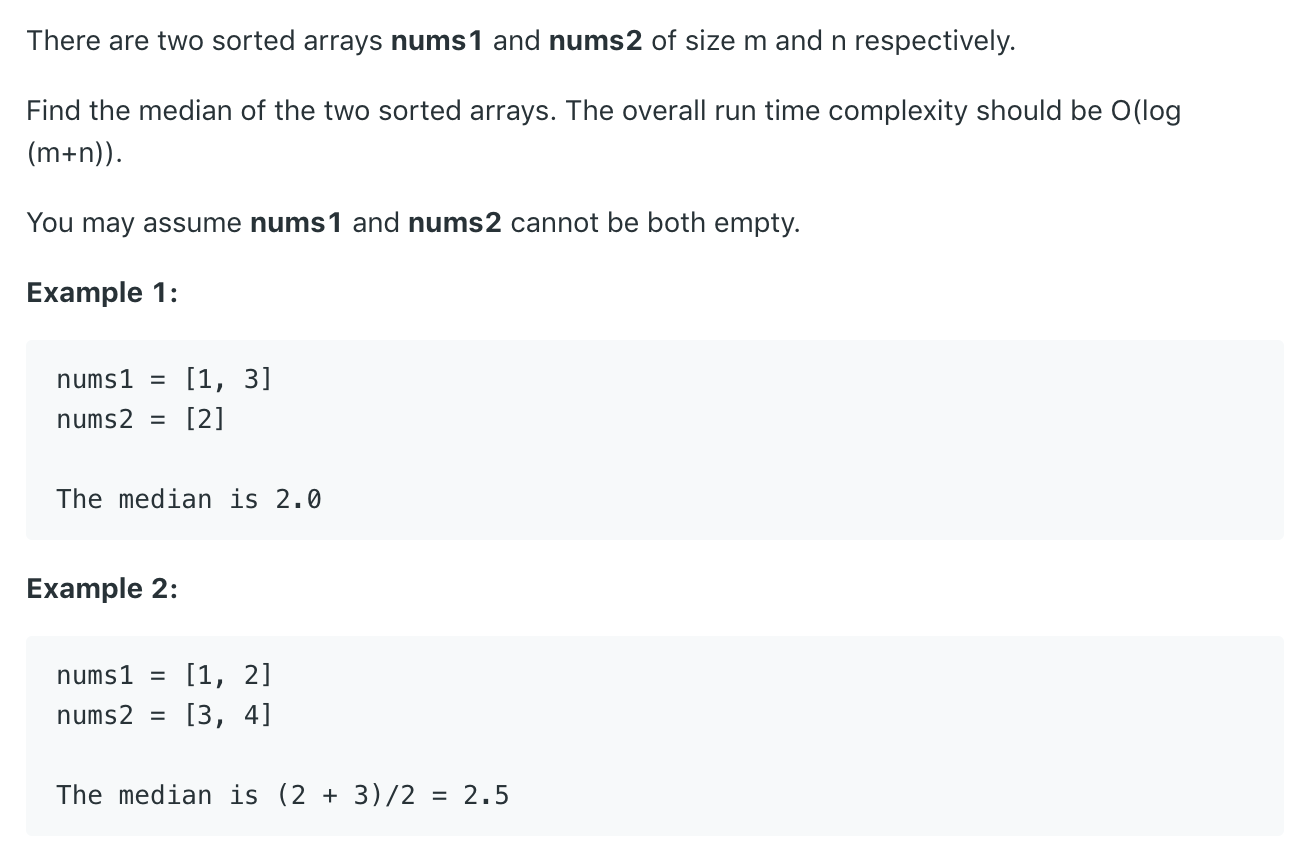
描述

Median of Two Sorted Arrays

算法

  • 核心思想：由于时间复杂度为 O(logn)，肯定还是得用二分搜索实现
    • 但是这次，我们需要同时对两个数组使用二分搜索
    • 每次搜索的时候，我们都区分出两个大小相等的部分（或者 left - right = 1）
    • 想象有上下两个数组，然后划一刀，将数组分为左上、左下、右上、右下
    • 原本二分搜索比较当前节点和 target
    • 而我们现在比较这四个角与target
  • 首先，我们要保证 num1 的长度比 num2 短，因此如果反了的话，则返回当前函数，并且参数交换
  • 计算左侧部分的元素数量，total = (len1 + len2 + 1) / 2
  • While l <= r || r < 0 || l >= len1，条件和普通的二叉搜索差不多，但是 l 和 r 自身有限制
    • 对 nums1 施展二分搜索，找到的位置便是左上角，然后根据这个位置计算出四个角落的位置
      • topLeft = (l + r) / 2
        • 如果 topLeft < 0，说明这一刀划在了 nums1 的开头
        • 因此需要设置 nums[topLeft] = -∞，来保证左上的元素 < 右下的元素
      • topRight = topLeft + 1
        • 如果 topRight >= len1，说明这一刀划在了 nums1 的结尾
        • 因此需要设置 nums[topRight] = ∞，来保证右上的元素 > 左下的元素
      • bottomLeft = total - topLeft - 2
        • 如果 bottomLeft < 0，说明这一刀划在了 num2 的开头
        • 因此需要设置 nums[bottomLeft] = -∞，来保证左下的元素 < 右上的元素
      • bottomRight = bottomLeft + 1
        • 如果 bottomRight >= len2，说明这一刀划在了 nums2 的结尾
        • 因此需要设置 nums[bottomRight] = ∞，来保证右下的元素 > 左上的元素
    • 在把四个角落都设置好之后，再开始比较
      • 如果 nums1[topLeft] <= nums2[bottomRight] && nums2[bottomLeft] <= nums1[topRight]
        • 目前我们处于正确的位置，中位数就在这四个角落里诞生
        • 如果这俩数组的长度之和为奇数，返回 max(nums1[topLeft], nums2[bottomLeft])
        • 如果这俩数组的长度之和为偶数，返回 (max(nums1[topLeft], nums2[bottomLeft]) + min(nums1[topRight], nums2[bottomRight])) / 2
      • 如果 nums1[topLeft] > nums2[bottomRight]，设置 r = topLeft - 1，相当于把刀逆时针旋转
      • 如果 nums2[bottomLeft] > nums1[topRight]，设置 l = topLeft + 1，相当于把刀顺时针旋转
    • 继续施展二分搜索，直到找到中位数

代码

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function(nums1, nums2) {
    // edge case
    if (!nums1.length) {
        const len = nums2.length;
        if (len % 2 === 0) return (nums2[len/2-1] + nums2[len/2]) / 2;
        else return nums2[parseInt(len / 2)];
    }
    if (!nums2.length) {
        const len = nums1.length;
        if (len % 2 === 0) return (nums1[len/2-1] + nums1[len/2]) / 2;
        else return nums1[parseInt(len / 2)];
    }
    
    const len1 = nums1.length, len2 = nums2.length;
    // 反向调用，保证 num1 更短
    if (len1 > len2) return findMedianSortedArrays(nums2, nums1);
    
    const total = parseInt((len1 + len2 + 1) / 2);
    // 根据 nums1，施展二分搜索
    let l = 0, r = len1 - 1;
    while (l <= r || r < 0 || l >= len1) {
        const topMid = Math.floor((l + r) / 2);
        const botMid = total - topMid - 2;
        
        const topLeft = topMid >= 0 ? nums1[topMid] : -Number.MAX_VALUE;
        const topRight = topMid+1 < len1 ? nums1[topMid+1] : Number.MAX_VALUE;
        const botLeft = botMid >= 0 ? nums2[botMid] : -Number.MAX_VALUE;
        const botRight = botMid+1 < len2 ? nums2[botMid+1] : Number.MAX_VALUE;

        // 如果目前的位置正确
        if (topLeft <= botRight &&
            botLeft <= topRight) 
        {
            if ((len1 + len2) % 2 === 1) {
                return Math.max(topLeft, botLeft);
            } else {
                return (Math.max(topLeft, botLeft) +
                        Math.min(topRight, botRight)) / 2;
            }
        } else if (botLeft > topRight) {
            l = topMid + 1;
        } else {
            r = topMid - 1;
        }
    }
};