Lynch

乘积最大子序列

Posted: 09.20.2019

#LeetCode #Top 100 Liked #面试问题 - 算法

描述

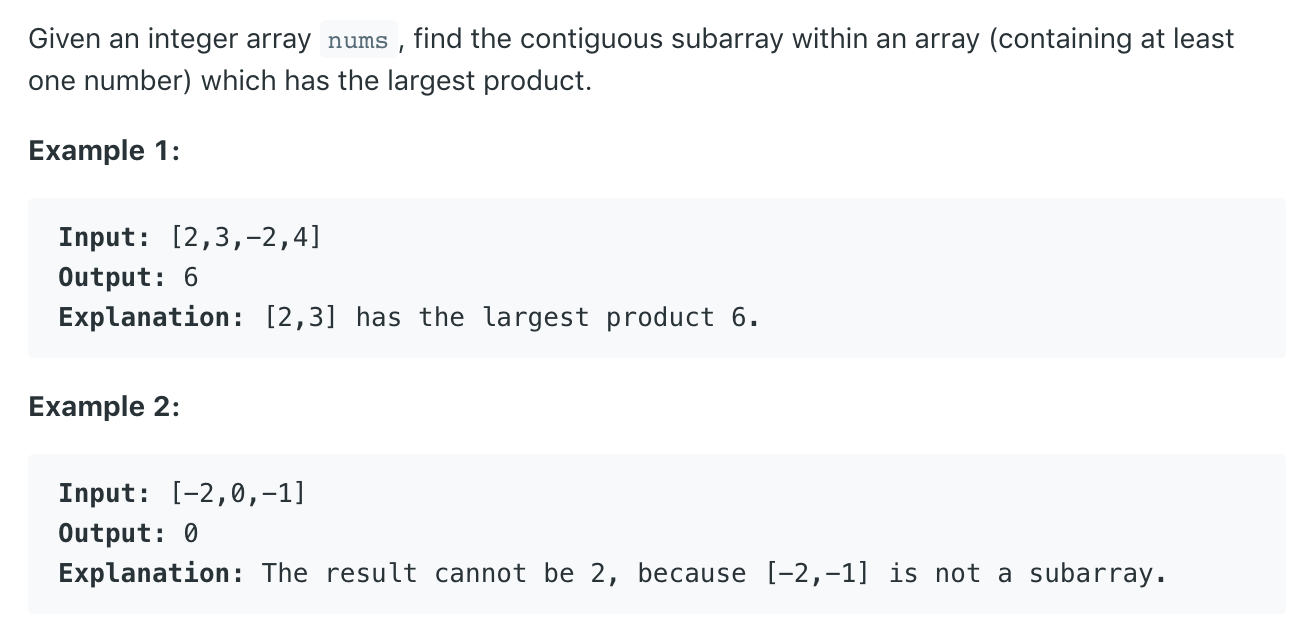
Maximum Product Subarray

算法

这个算法是我自己发明的，和官方的答案不一样

  • 核心思想是，一直记录正的乘积以及负的乘积
    • 因为我们要求的是成绩最大的子序列，所以如果把正的乘积与负的乘积与当前元素相乘（0 除外）
    • 要么正的乘积增加了，或者不变（1 或者 -1）
    • 要么负的乘积的绝对值增加了，或者不变（1 或者 -1）
    • 因此，这就意味着，每个非 0 的元素都是有用的
  • 设置 posCurr = negCurr = 1，用来记录当前为止，正的乘积与负的乘积
  • 遍历数组
    • 首先先查看 posCurr 和 negCurr 是否合法
      • If posCurr < 0，那它不合法，因此设置 posCurr = 1
      • If negCurr > 0，那它不合法，因此设置 negCurr = 1
    • 如果当前元素为 0
      • 那么当前为止正的乘积与负的乘积都断了
      • 因此设置 posCurr = negCurr = 0
    • 如果当前元素是正数
      • 正的乘积会变得更大：posCurr = posCurr * curr
      • 负的乘积绝对值也会变得更大：negCurr = negCurr * curr
    • 如果当前元素是负数
      • 需要通过与负的乘积相乘来得到正的乘积：posCurr = negCurr * curr
      • 需要通过与正的乘积相乘来得到负的乘积：negCurr = posCurr * curr
    • 查看 posCurr 是否 > max，如果是的话就更新 max

代码

/**
 * @param {number[]} nums
 * @return {number}
 */
var maxProduct = function(nums) {
    // edge case
    if (!nums || !nums.length) return 0;
    
    let posCurr = negCurr = 1,
        _max = -Number.MAX_VALUE;
    for (let i = 0; i < nums.length; i++) {
        const num = nums[i];
        posCurr = posCurr <= 0 ? 1 : posCurr;
        negCurr = negCurr >= 0 ? 1 : negCurr;
        if (num === 0) {
            posCurr = negCurr = 0;
        } else if (num < 0) {
            const temp = negCurr;
            negCurr = posCurr * num;
            posCurr = temp * num;
        } else {
            posCurr = posCurr * num;
            negCurr = negCurr * num;
        }

        _max = Math.max(posCurr, _max);
    }
    
    return _max;
};